Diagram 1:
OUCC Proceedings 9 (1979)A Computer goes Surveying |
OUCC Proceedings 9 Index |
by Colin Nicholls
Many people have quoted the use of a computer in the processing of cave surveying data (Refs. 1-4) but, despite claims of Ellis, as far as I know only Wilcock has produced a program listing and this program did not include a loop misclosure routine. There are good reasons why listing is of limited value:- there will be language incompatibilities between machines and most people with access to a computer will be able to write their own program. It is also possible that authors will not want to admit in print that they have used someone else's expensive computing time for their own ends.
However, in this article I give a listing in BASIC (a widely used language with only minor differences between machines) and flow chart (of sorts) which together should enable a surveyor to adapt this program for his specific requirements. I also hope that publishing this program could save a surveyor considerable time and effort. I told the Editor that I could write a program in a morning (after all it's only a spherical polar/rectangular Cartesian conversion, isn't it?). To date I have been working on it on and off for two months. Even so, the program presented is not completely optimised, takes a hefty chunk of memory (about 19K) on our Research Machines 380Z microcomputer) and requires some thought when dealing with very complicated passage (e.g. loops on loops on loops), but it does work and starting with distance, bearing and inclination readings it will give the x, y and z co-ordinates of the survey station; the extended elevation data; the co-ordinates of the point projected onto any vertical plane; will close loops using an equal distribution of errors on each leg and will give the loop misclosure errors.
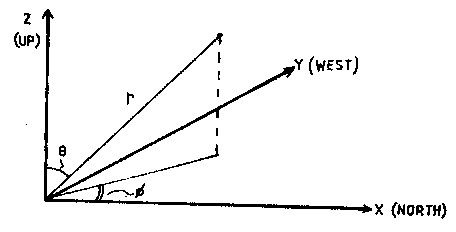
The standard method of cave surveying using a tape measure (to obtain distance), a compass (for bearings) and an inclinometer (for inclination) gives form of Spherical Polar Co-ordinates. In fact:
| D = r | B = j | I = 90 - q |
D is distance, B is the bearing and I is the inclination and r, q and j are the usual Spherical Polar co-ordinates (see diagram 1):-
Diagram 1: |
 |
A little "A" level maths shows that the changes in x, y, and z, D x, D y and D z respectively between two stations whose readings are taken as D, B, and I are
| D x= Dcos(I).cos(B) | D y = Dcos(I).sin(B) | D z = Dsin(I) |
If we then assume that the entrance has co-ordinates (0, 0, 0), we can work out the co-ordinates of the first station by adding the first D x, D y and D z to the co-ordinates of the entrance station. The second station's co-ordinates can be found by adding the second D x, D y and D z to the co-ordinates of the first station. In this cumulative way we can determine the co-ordinates of stations further down the cave.
Consider a passage which forks and then rejoins itself as in diagram 2:-
Diagram 2: |
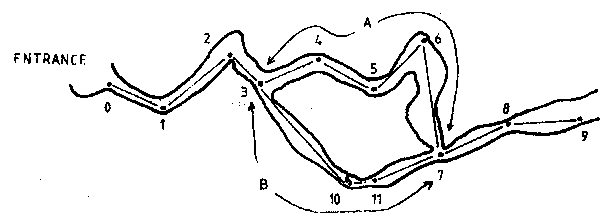 |
Using the techniques just described, we can find the co-ordinates of all the stations from 0-9. If we now restart from station 3 and this time survey around path B we again reach station 7, and since we know the co-ordinates of 3, we can deduce the co-ordinates of station 10, 11 and 7. This gives two ways of finding the co-ordinates of 7:- surveying via path A or path B.
Obviously station 7 is in the same place whichever way round the loop we survey and so we should hope that the co-ordinates obtained via the two paths are the same. Unfortunately, any survey is to some degree inaccurate and therefore will get two values for the co-ordinates of station 7, either of which could be right, or more likely, wrong. There are several ways of correcting for this error (Refs. 4 and 5).We, of course, chose the simplest. Ellis (Ref. 6) claims there to be little difference between any method, so why not chose the easiest?
In this method the difference between the two sets of co-ordinates representing point 7 is divided into N equal parts, where N is the total number of legs around the loop (in diagram 2 path A has 4 legs and path B has 3, making a total of 7). If we call the size of one of these parts E, then we assume each leg is wrong by E, and hence add this on to all the readings.
Thus we assume that the co-ordinates of point 3 are correct but that the readings from 3 to 4 were wrong by E. Hence station 4 is shifted by an amount E. The readings from 4 to 5 were also wrong by E and thus station 5 is moved by 2E. One lot of E due to the error in the readings from 4 to 5, and another E because station 4 was also in error by E.
In this way station 4 is wrong by E, station 5 by 2E, station 6 by 3E and station 7 by 4E. Going round path B station 10 is out by E, station 11 by 2E and station 7 by 3E. In this way the two values for the co-ordinates for station 7 are averaged to give the corrected values.
All points past station 7 (i.e. station 8 onwards) have to be corrected by the same amount (i.e. 4E if their co-ordinates were derived by surveying via path A or 3E if they were derived via path B).
To avoid having to tell the computer if the readings are forward or back bearings in this program the computer assumes that the higher the station number, the further into the cave the station is. The difference in station number between adjacent stations does not have to be one provided that the highest number is furthest down the cave.
Thus the problem arises in diagram 2. Readings taken from station 11 to station 7 are forward bearings, whereas since 7 is less than 11 the computer will think of them as back bearings.
Since the program closes the loops between specified stations, and does not close the loop onto a station with the same number, one station may have two numbers according to the path via which it is reached. For example, we could number station 7 as station 12 when surveying around path B. The computer will close the loop between stations 7 and 12 (see section 3d). It would therefore have been possible, but even more confusing, to label stations 3, 10, 11 and 12 in path B as 3, 4, 5 and 6 if desired.
Since the computer needs to remember the original co-ordinates of the stations to correct them, the co-ordinates of the station on path A and B have to be kept separate. This is done by storing the co-ordinates of the first path in the computer arrays with locations from 0 to 99, with the stations on the second path stored in locations 100 onwards.
The order in which the blocks are given follows the order in which the computer does them. The letter beside the block designates that block in the program listing (note: program listing was too poor a quality to be reproducible here).
Blocksa) The arrays are initialised, subject to a maximum of a 100 points in the first branch of the loop and 150 in the second branch. The cave name and the number of stations in the first branch are entered, as are the co-ordinates and the number of first station. These can be set to (0, 0, 0, 0) at the entrance or to the previously derived figures if the branch is part way down the cave.
j)(The calculation subroutine.) For each set of readings (distance, bearing, and inclination) the starting station and the finishing station are specified as well as the recorded readings. When all the readings for one particular section of the cave have been entered (determined by the entered value of the total number of stations in the first branch) all the readings are printed out to allow any typing errors to be found and corrected. The incremental increases in X, Y, and Z, the extended elevation co-ordinates and the total leg plan lengths are calculated.
b) The required number of copies of the data is put in and the print subroutine is called.
k) The incremental co-ordinates are added to the co-ordinates of the previous station to obtain the co-ordinates of the next station. The results are printed out, rounded to one decimal place, along with the total surveyed leg length and plan length.
c) The program asks if there are any loops - Y (yes) going to block (d), N (no) going to block (g).
d) The first and last stations in the loop are entered (i.e. 3 and 7 in diagram 2) along with the number of stations in the second branch (4-3, 10, 11 and 12). The station number of the first station in the second branch is entered and the program goes through the subroutines for calculation and printout.
e) The differences in the X, Y, and Z positions of the final point are calculated as is the total error (called E in the program). The loop is then closed as described in section 2. The total correction E is added to all the points after the loop has closed since these have to be shifted down by this amount (i.e. station 8 onwards).
The printout routine is called twice to print the corrected data for the first and second legs (branches).
f) The total loop misclosure error (E) is printed as is the error expressed as a percentage of the total distance round the loop.
g) The required number of projections onto a vertical plane is entered. P1=0 going to block (i).
h) The angle of the plane is entered and the projected length, height, extended elevation and station numbers are printed. This enables projected elevations to be drawn.
i) All the data is loaded onto a cassette for the fast retrieval and easy access for further processing.
As mentioned previously, this program is published in the hope that it will provide a reasonable basis for adaptation. I therefore feel some comments on the difficulties encountered and possible extensions might be of value.
The main problems in writing this program were concerned with keeping the data from paths around a loop separate, whilst at the same time only including one calculation and open print subroutine. The essential problem here was in getting the starting and finishing values for the various 'I' loops correct - hence the abundance of J's, F's, I1's, I2's etc.
To keep the different path data separate I chose the apparently clumsy method of using one array, but fixing locations at which the data was restricted according to path. The advantage of this, is that all X co-ordinates say, which all require the same processing, are in one array. Hence only the location values need be changed rather than the array names.
There are many possible extensions to the program e.g. subroutines to calculate bearing from origin, total passage lengths in any given direction etc. (See Ref. 2 for more examples), but the routines in this program are sufficient to enable a basic survey to be drawn from the original data. Besides which the extensions are easily included into the program in much the same way as the projection routine (block h) is included in this version.
I purposely did not get the computer to plot the survey stations as I felt the resulting mess of dots would be confusing unless they were labelled or the skeletal line of site plot was done at the same time. I think it is probably a lot quicker and in the long run will produce a clearer survey if the surveyor plots his own survey from the list of co-ordinates.
| Ellis, B.M. Surveying Caves | Introductory work, fairly comprehensive |
| Transactions of the CRG (1970) 12, 3 | Interesting volume. Concerns some of the more academic points |
| Hanna, K (1964) 'The Survey' Proc. UBSS. 10, 285 | |
| Gardner, J.W. (1971) Jour. LUSS. 1, 26-29 | Contains only an output listing, not as Ellis claims, a program. |
| O'Reilly, P.M. (1970) Trans. CRG 12, 149-154 | Although the article claims a listing 'below' none appears. |
| Wilcock, J.D. (1970) Trans. CRG 12, 211-219 | A program in Algol 60 is listed. |
| Irwin and Stener. (1975) Trans. BCRA 2, 4 | |
| Ellis, B.M. (1966) Jour. Shepton Mallet CC 4, 2 10-20 |