Corrosion for Cavers I
Some Aspects of the
Corrosion of Caving Ladders
Andy Riley
In a short article it is difficult to deal with corrosion in a thorough manner, as it is an exceedingly complex and as yet not well understood science. However, I hope to make cavers aware of some of the basic electrochemical and metallurgical ideas in the theory of corrosion as applied to caving equipment.
Any metal or combination of metals when immersed in solution attains an equilibrium, or corrosion, potential which can be measured against another fixed reference electrode in the same solution. This potential is what is known as a 'mixed’ potential and is the result of the addition of all the potentials caused by anodic and cathodic reactions on the metal object's surface. In any example of corrosion there has to be at least one cathodic and one anodic reaction. A cathodic reaction is one which uses up electrons (a reduction) and an anodic reaction is one which liberates electrons (an oxidation). Because there must never be a net surplus or deficit of electrons, the total cathodic current must exactly balance the anodic current. On a metal surface, for instance iron, several reactions are possible (Figure 1).
E1 Fe = Fe2+ + 2e (1)
E2 O2 + 2H2O + 4e = 4OH- (2)
where E1 and E2 are the reversible potentials for the reactions.
What determines which will be the cathodic or anodic reaction is the relative sizes of the reversible potentials (Appendix 1) for these reactions. If E2 is more positive (or noble) than e1, then reaction 2 will be cathodic to reaction (1) and vice versa. This is the case in practice as E1 = -0.44V and E2 = +0.790V in household tap water (pH 7). This means that iron dissolves or corrodes away. The problem the corrosion scientist has is to measure how fast the iron is corroding. He cannot measure the corrosion current with a meter as he cannot physically separate the anodic and cathodic sites on a metal surface. He has therefore to employ some other means (Appendix 2).
Both the anodic and cathodic reactions obey an equation which relates current (how fast they go) with potential (driving force). This is the Tafel equation:
E = b.log(i) + a (3)
where i = current, E = potential and a and b are constants: b is the Tafel slope, used in Appendix 3.
When we plot these corrosion reactions on a log current-potential graph we have what is known as an Evans Diagram. It is now easy to see that the corrosion potential is the potential where the two currents are equal and opposite (Figure 2). This is the corrosion current. In all cases the reaction which is the slowest or hardest to occur for a given potential dominates the corrosion process and in most cases this is a cathodic reaction, the reduction of O2. This is because the diffusion of oxygen to the metal surface is the rate controlling step. The effect of increasing the availability of O2 can be easily shown in an Evans Diagram and has the effect of increasing the corrosion current by raising the corrosion potential (Figure 3).
This is the reason why moist surfaces corrode faster than those totally immersed: there is a greater availability of oxygen. Turbulent waters (e.g. cave streams) have a higher O2 content than stagnant water and hence corrosion will proceed at a faster rate.
The phenomenon of galvanic protection is a more complicated case of mixed potentials. It is often assumed that inspection of a table of standard Nernstian potentials of metallic elements will determine which metal will be the anode and which the cathode in a bimetallic couple. In most situations this is not the case. The Evans Diagram for a zinc and iron couple demonstrates the complexity (Figure 4). The size of the corrosion current is determined by the sum of all the cathodic and anodic areas (Appendix 3).
I shall now discuss the case of a caving ladder as an example of a situation where three metals, iron, aluminium and zinc, are in contact.
Zinc is applied to steel wires (British Standard BS443) with the intention of cathodically protecting the base metal, in other words, the zinc acts as a sacrificial coating. The potential of zinc is normally lower than that of iron and steel and hence it will act as an anode and preferentially dissolves instead of iron. However, the rate of dissolution depends on several conditions, including the pH, oxygen content and temperature of the liquid environment. Figure 5 shows the pH dependence of the rate of loss of the zinc coating.
In aerated water it is possible to get a reversal of polarity (Uhlig, 1971) between zinc and iron, making the zinc more noble than the iron, and pitting of the base metal can result. Waters high in carbonates and nitrates can assist in this reversal, due to the formation of a ZnO film on the zinc instead of Zn(OH)2 (Rowe and Walker, 1961). The ZnO is a semiconductor which is electrically conducting and behaves as an oxygen electrode whose potential is more noble than zinc or iron. Bicarbonate ions (as found in cave water) have been shown to stimulate the production of ZnO.
It is important to note that galvanic protection is only really effective if the object is totally immersed, and the water should have adequate conductivity. In water of low conductivity (e.g. distilled or soft waters) any defect in the coating greater than a millimetre in size will not be protected at its centre and the underlying metal will corrode. This is because the current density sufficient to protect the underlying metal cannot be maintained over the entire surface.
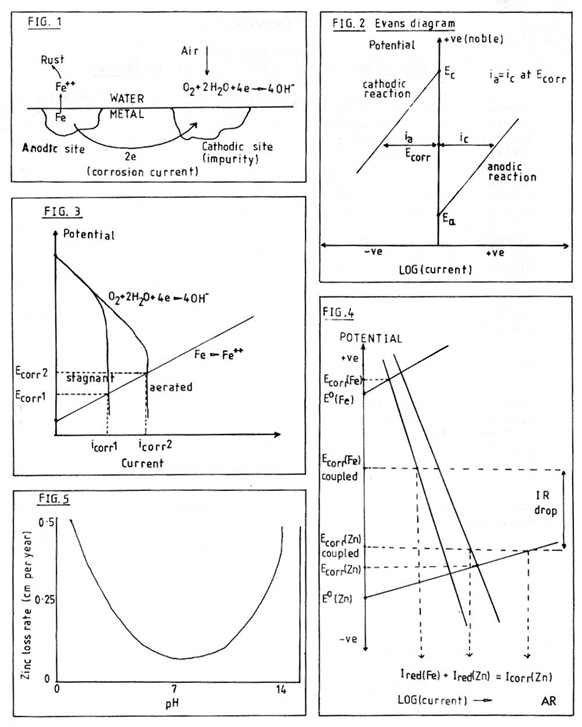
The coupling of aluminium rungs to the galvanised wires has the effect of raising the corrosion potential of the wire. I have measured the corrosion potentials of an aluminium rung and a piece of ladder wire in cave water. The rung had a potential of -0.578 V/SCE* and the steel wire -0.810 V/SCE. The corrosion potential of a piece of ladder (rung and wire) was -0.724 V/SCE. Aluminium has a passive film on its surface which causes it to have a potential much more noble than expected from a table of metal electrode potentials. By raising the corrosion potential the corrosion rate on the galvanised wire has also been increased (Figure 6). In other words, the use of aluminium rungs makes the ladder wires corrode more quickly.
Because of the traditional method of coiling ladders, the ends of the wires undergo a lot of flexing, which fractures and flakes off the brittle hot-dipped zinc coating. This can create large coating defects which will not be protected and corrosion attack will be intense and localised, leading to eventual failure. It is recommended that another method be used, perhaps coiling ladders loosely, and then carrying them in a tackle bag.
* All electrode potentials must be measured with respect to a reference electrode, which in this case is a standard Calomel electrode (SCE), i.e. V/SCE = volts with respect to the SCE.
Appendix 1
The Nernst equation defines the equilibrium thermodynamic potential of a metal in contact with a solution of known concentration of metal ions.
![]() (4)
(4)
E° is the standard potential, T is the absolute temperature and z the number of electrons involved in the redox couple.
Appendix 2
Measurement of the corrosion current can be made using the Stern equation
![]() (5)
(5)
A small potential shift (DE) is made from the corrosion potential and a change in current (DI) is produced. By measuring the anodic and cathodic Tafel slopes (ba and bc) one can estimate Icorr (see equation (3) for definition of b).
Appendix 3
![]() (6)
(6)
The total current on any site depends on the current density (iJa) and its area (fj). Rewriting equation (6),
![]() (7)
(7)
Corrosion on a polyelectrode can be represented by
![]() (8)
(8)
B = base, N = noble, a = anodic, c = cathodic, i = current, f = area.
Galvanic protection occurs chiefly when fN is much greater than fB and therefore iNa tends to 0 and iBa tends to |iBa|.
References
(For a general review of corrosion, see Shreir (1976) and West (1970) ).
British Standard BS443.
Rowe , L. C. and Walker, M.S., 1961. Effect of mineral impurities in water on the corrosion of aluminium and steel. Corrosion 17, 353t-356t.
Shreir, L. L. , 1976. Corrosion. Butterworth, London, 2 vols. , 2nd edn.
Uhlig, H.H. , 1971. Corrosion and Corrosion Control. Wiley, New York, 2nd edn.
West, J.M. , 1970. Electrodeposition and corrosion processes. Van Nostrand, London, 2nd edn.